Evualuaciòn de Polinomios

Evaluar un polinomio 

Evaluar un polinomio consiste en determinar qué valor toma el polinomio cuando la indeterminada (x) se sustituye por un número. 

Consideramos el polinomio P(x)=2x³-5x+3 evaluar el polinomio en 1 consiste en sustituir la indeterminada por 1 (x=1) quedando P(1)=2·1³-5·1+3=2-5+3=0.

Teorema del resto

El valor que se obtiene al evaluar un polinomio en x=a coincide con el resto de dividir ese polinomio por x-a. 

Si dividimos un polinomio P(x) por x-a se obtendrá un cociente C(x) y un resto r. 

En toda división el dividendo P(x) es igual al divisor x-a por el cociente C(x) más el resto r , es decir,P(x)=(x-a)·C(x) + r.

Al evaluar el polinomio en el punto se tiene 

P(a)=(a-a)·C(a) + r , como a-a =0 entonces P(a) = r 

Gracias a este teorema podemos usar la regla de Ruffini para evaluar un polinomio en un punto.

Ejercicios:

 en 

 P(0)=2(0)4 03-8(0)2 -8(0)+8 

 P(0)=-8

Evalúa el polinomio P(x)=2x³-5x+3 en x=1 usando la regla de Ruffini 

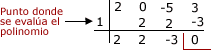
P(1) = 0 ya que 0 es el resto de la división de P(x) entre x-a