Funciones Racionales

Es el cociente entre dos funciones polinomiales.El dividendo se llama numerador, y el divisor, denominador:

 

 La palabra "racional" hace referencia a que la función racional es una razón o cociente (de dos polinomios); los coeficientes de los polinomios pueden ser números racionales o no.El denominador, D(x) nunca es la funcion polinomial cero.

 Las funciones racionales tienen diversas aplicaciones en el campo del análisis numérico para interpolar o aproximar los resultados de otras funciones más complejas, ya que son computacionalmente simples de calcular como los polinomios, pero permiten expresar una mayor variedad de comportamientos.

Propiedades:

• Toda función racional es de clase ${\displaystyle C^{\infty }}$ en un dominio que no incluya las raíces del polinomio Q(x).
• Todas las funciones racionales en las que el grado de Q sea mayor o igual que el grado de P tienen asíntotas (verticales, horizontales u oblicuas).
• Todas las funciones racionales cuyos coeficientes pertenecen a un cuerpo forman un cuerpo que incluye al cuerpo base como subcuerpo. El cuerpo de funciones racionales forma un subcuerpo del cuerpo de series de potencias formales.

El dominio de una función racional de lo forman todos los números reales menos los valores de x que anulan el denominador.

Ejemplos:

 

Un tipo de función racional es la función de proporcionalidad inversa de ecuación:

  .

Construcción de hipérbolas

Las hipérbolas   son las más sencillas de representar.

Sus asítontas son los ejes

El centro de la hipérbola, que es el punto donde se cortan las asíntotas, es el origen.

A partir de estas hipérbolas se obtienen otras por traslación.

1. Traslación vertical

El centro de la hipérbola es: (0, a).

Si a>0, se desplaza hacia arriba a unidades.

El centro de la hipérbola es: (0, 3)

Si a<0, se desplaza hacia abajo a unidades.

El centro de la hipérbola es: (0, -3)

2. Traslación horizontal

El centro de la hipérbola es: (-b, 0).

Si b> 0, se desplaza a la izquierda b unidades.

El centro de la hipérbola es: (-3, 0)

Si b<0, se desplaza a la derecha b unidades.

El centro de la hipérbola es: (3, 0)

3. Traslación oblicua

El centro de la hipérbola es: (-b, a)

El centro de la hipérbola es: (3, 4).

Para representar hipérbolas del tipo:

se divide y se escribe como:

Su representación gráfica es una hipérbola de centro (-b, a) y de asíntotas paralelas a los ejes.

El centro de la hipérbola es: (-1, 3)

 Video. desde youtube:

 Invistagaciones: http://www.ditutor.com/funciones/funcion_racional.html

Con mas informacion revisar mi blogger

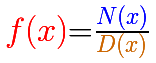
Graficacion de Polinomios

Si  an es el coeficiente principal de un polinomio de un grado n; entonces, tenemos el siguiente criterio determinar la forma de gráfico de polinomio:

Si n es impar 

Si an > 0, el gráfico es decreciente a la izquierda  y creciente a la derecha ; es decir cuando x ->-α

Si an < 0, el gráfico es creciente a la izquierda y decreciente a la derecha

Si n es par 

Si an > 0, el gráfico es creciente a la izquierda  y creciente a la derecha

Si an < 0, el gráfico es decreciente a la izquierda y decreciente a la derecha

para graficar los polinomios hay que seguir lo siguiente:

venida de: ejercicios2bachillerato.blogspot.com

1. Prediga el comportamiento final de la función.

2. Encuentre los ceros reales de la función. Compruebe si es posible de reescribir la función en forma factorizada para encontrar los ceros. De otra manera, use la regla de los signos de Descartes para identificar el número posible de ceros reales.

3. Haga una tabla de valores para encontrar varios puntos.

4. Grafique los puntos y dibuje una curva continua suave para conectar los puntos.

5. Asegúrese que la gráfica sigue el comportamiento final como se predijo en pasos anteriores.

Ejemplo:

Grafique la función polinomial x³ – 2x² – 3x .

Prediga el comportamiento final de la función.

El grado de la función polinomial es impar y el coeficiente principal es positivo.

El grado del polinomio es 3 y habría 3 ceros para las funciones.

La función puede factorizarse como x ( x + 1)( x – 3). Así, los ceros de las funciones son x = –1, 0 y 3.

Haga una tabla de valores para encontrar varios puntos.

Grafique los puntos y dibuje una curva continua suave para conectar los puntos

venida,de:http://hotmath.com/hotmath_help/spanish/topics/graphing-polynomial-functions.html 

mas información revisar este siguiente video de youtube:

Por favor revisar y dejar sus comentarios me servirá de mucha ayuda para mejor mi blogger espero que sea de mucha ayuda

ejercicios2bachillerato.blogspot.com

Raíces de una Ecuación Polinomial

Raíces Racionales  de un polinomio

Formula:

 Si a₀ y a_n son diferentes de cero, entonces cada solución racional x, cuando está escrita como fracción irreducible x = p/q, satisface

• p es un factor del término constante a₀, y
• q es un factor del coeficiente del término a_n.
• p y q son oprimimos:

Así, una lista de las posibles raíces racionales de la ecuación se puede derivar usando la fórmula ${\displaystyle x=\pm {\frac {p}{q}}}$.

El teorema de la raíz racional es un caso especial (para un solo factor lineal) del lema de Gauchos en la factorización de polinomios. El teorema de la raíz entera es un caso especial del teorema de la raíz racional si el coeficiente principal a_n = 1.

1)Para calcular las raíces enteras hay que sacar el divisor:

Divisores a0

Divisores an

Ejercicios:

P(X)=3X3+2X2-7X+2

DIVISORES: 3X3= +1; +3          +2     =  +1; +2

Divisores a0                      +1; +2                  =        +1; +1 ; +2; +2

Divisores an                      +1; +3                                   3           3

+1

                                      3X3+2X2-7X+2

=3(1)3+2(1)2-7(1)+2                          =3(-1)3+2(-1)2-7(-1)+2                  

=3(1)+2(1)-7+2                                 =3(-1)+2(1)+7+2   

=3+2-7+2                                          = -3+2+7+2

=0  -> Si es raíz                                = 8 -> No es raíz

+  1

    3

                                       3X3+2X2-7X+2  

=3(1)3+2(1)2-7(1)+2                             =3(-1)3+2(-1)2-7(-1)+2                                 

     3        3       3                                         3         3        3

=3(1)+2(1)-7+2                                  =3(-1)+2(1)+7+2                                  

    27     9   3                                            27     9    3

= 1+ 2 -7+2                                       = -1 + 2 + 7 + 2

   9   9  3                                               9     9    3

 = 3 -7 +2                                         =  -1 + 7 +2

    9  3                                                    9    3

=  1 - 7 + 2                                       = 1+21+18

    3   3                                                      9

= -6 +2                                             =  40 /9 -> No es raíz

    3 

=-2+2 =0    ->Si es raíz

+2

3X3+2X2-7X+2

  = 3(2)3+2(2)2-7(2)+2                                            = 3(-2)3+2(-2)2-7(-2)+2

  = 3(8)+2(4)-14+2                                                 = 3(-8)+2(4)+14+2

  = 24+8-14+2                                                       = -24+8+14+2

  = 34-14                                                               = -24+24 

  =20 -> No es raíz                                                = 0  -> Si es raíz

Hasta aquí nomas se realiza ya que ya encuentre 3 divisores que salen o entonces los demás ya no se hacen suficiente con lo  que hicimos 

         RST=   X1=   +1     

                     X2=    +1

                                3 

                     X3=   -2

Ejm: Utilizando el Teorema del Factor y la División  Sintética

https://youtu.be/qqbiO4ae1Bk

1) Escribe una lista de las posibles raíces racionales de un polinomio

2) Factorice completamente cada Polinomio

Dirrecion de la información de    Utilizando el Teorema del Factor y la División  Sintética

http://www.matematicatuya.com/NIVELACION/ALGEBRA/S8.html

Con mas informacion ir a mi blogger:
ejercicios2bachillerato.blogspot.com

Raíces de  una Ecuación Polinomial

Raíces enteras

Las raíces enteras son las que  salen como resultado es P(x)=0 así como el siguiente:
EJM:

P(x)=2x3-x2-4x+3                                                         Divisiones (+1 ; +3)
P(1)=2(1)3-(1)2-4(1)+3
       =2-1-4+3
       =2-5+3
       =0               Si es raíz
x= -1
P(-1)=2(-1)3-(-1)2-4(-1)+3
        =2(-1)-(1)+4+3
        = -2-1+4+3
       =-3+7
       =4                No es raíz
x= +3
P(3)=2(3)3-(3)2-4(3)+3
       =2(27)-9-12+3
       =54-9-12+3
       =57-21
       =36            No es raíz
x= -3
P(-3)=2(-3)3-(-3)2-4(-3)+3
       =2(-27)-9+12+3
       = -54-9+12+3
      =-63+15
       =-48       No es raíz
 R= La raíz entera en x= +1

Ejercicios : 

P(x)=x3+x2-4x-4=0                                                          Divisiones ( +1;+2;+4)
  
x=+1
P(1)=(1)3+(1)2-4(1)-4
      =1+1-4-4
      =2-8
      =-6     No es raíz

x= -1
P(-1)=(-1)3+(-1)2-4(-1)-4
        =-1+1+4-4
       =-5+5
      =0      Si es raíz
x=+2
P(2)=(2)3+(2)2-4(2)-4
       =8+4-8-4
       =0    Si es raíz
 x=-2
P(-2)=(-2)3+(-2)2-4(-2)-4
        =-8+4+8-4
        =-12+12
       =0      Si es raíz
x=+4
P(4)=(4)3+(4)2-4(4)-4
        =64+16-16-4
        =80-20
        =60       No es raiz
x= -4
P(-4)=(-4)3+(-4)2-4(-4)-4
        =-64+16+16-4
        =-68+32
        =36         No es raiz
R=La respuesta es x= -1    x= +2      x= -2

Aquí se encuentra un vídeo para que se fijen   :

https://youtu.be/s_k8Je0v434

Ecuaciones polinomiales

Pag: 45,46

FORMULA:
P(x)=anxn+anxn-1 +...........+a1x+a0=0

Teorema del factor 

En álgebra, el teorema del factor sirve para encontrar los factores de un polinomio. Es un caso especial del teorema del resto.

ejm:
                                                     P(x)=2x2-3x-5                        a=-1  ->(x+1)
P(a)=o                                                                                         a=2.5 ->(x-2.5)
P(x)=2x2-3x-5
P(-1)=2(-1)2-3(-1)-5
        =2+3-5
        =0
P(x)=2x2-3x-5
P(2.5)=2(2.5)2-3(2.5)-5
         =2(6.25)-7.5-5
         =12.5-12.5
         =0
R= si son factores xq  si sale que P(x) es igual a 0

EJERCICIOS:

• Compruebar si x+3 y x-5 es factor del siguiente polinomio

P(x)=2x3+5x2-6x-7                            x+3     ->     x=-3
P(-3)=2(-3)3+5(-3)2-6(-3)-7 
        =2(-27)+5(9)+18-7
        = -54+45+18-7
        =-61+63
        =2
R= No es factor de x+3 xq no sale igual a 0
P(x)=2x3+5x2-6x-7                        x-5    ->    x=5
P(5)=2(5)3+5(5)2-6(5)-7 
      = 2(125)+5(25)-30-7
      =250+125-37
     =338
R=No es factor 
Para mejor entendimiento revisar este siguiente video:

https://youtu.be/q-i63N0t8gU

Para mas informacion sigua revisando mi blogg: ejercicios2bachillerato.blogspot.com